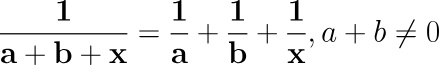Advanced Mathematics – Paper VI – WBCS Main Question Paper
Contents

WBCS Advanced Mathematics
Video explanations are given at the end of every year’s questions.
WBCS Main Question Paper – 2022
- In ΔABC, ∠B = 90° , AB = 12 cm, BC = 16 cm. The area of semicircle drawn on diameter AC is
(A) 157 cm²
(B) 314 cm²
(C) 150 cm²
(D) 328 cm²
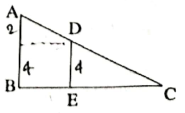
- In the given figures AB and DE are perpendiculars to BC. If AB = 6 cm, DE = 4 cm and AC = 15 cm, then CD = ?

(A) 5 cm
(B) 2 cm
(C) 10 cm
(D) 4 cm
- The hypotenuse of a right-angled triangle is 41 cm. The sum of the other sides is 49 cm. Then the area of the triangle is
(A) 360 cm²
(B) 720 cm²
(C) 180 cm²
(D) 120 cm²
- The roots of the quadratic equation

are
(A) a, b
(B) -a, b
(C) a, -b
(D) -a, -b
- If the centroid of the triangle formed by the points (a,b), (b,c) and (c,a) is the origin, then a3 + b3 +c3 = ____.
(A) abc
(B) 0
(C) a + b + c
(D) 3abc
- In a math lesson Shamali drew some triangles and some quadrilaterals. She drew 27 polygons altogether and a total of 99 vertices. Then total number of triangle she drew __
(A) 9
(B) 3
(C) 27
(D) 33
- The angles of a quadrilateral are in A.P. with common difference 20°. Then the smallest angle is
(A) 100°
(B) 130°
(C) 30°
(D) 60°
- A square lawn is bounded on three sides by a path 4 m wide. If the area of the path is ⅞ that of the lawn, then each side of the lawn is
(A) 10 m
(B) 12 m
(C) 16 m
(D) 18 m
- The volume of a cylinder of radius r is ¼ of the volume of a rectangular box with a square base of side length x. If the cylinder and the box have equal heights, what is the value of r in terms of x?
(A) x²/2π
(B) x/2√π
(C) √2x/π
(D) x/√π
- The hypotenuse of a right-angled triangle is 26 cm and the sum of other two sides is 34 cm. Then the lengths of the two sides are
(A) 10 cm, 24 cm
(B) 8 cm, 26 cm
(C) 12 cm, 22 cm
(D) 14 cm, 20 cm
- If LCM of f(x) and g(x) is 6×2+13x+6, then which of the following cannot be HCF of f(x) and g(x)?
(A) 2x+3
(B) 3x+1
(C) (2x+3)(3x+2)
(D) 3x+2
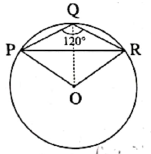
- In the given figure, ∠PQR = 120°, where P, Q and R are points on a circle with centre O. Then ∠OPR is

(A) 20°
(B) 10°
(C) 30°
(D) 40°
- A pole of length 12 m casts a shadow of length 15.3 m. Then the length of the shadow cast by another pole of length 18 m is
(A) 23.4 m
(B) 24 m
(C) 46.8 m
(D) 31.2 m
- A cuboid with length 14 cm and breadth 11 cm and a cylinder have the same height and volume. Then the radius of the base of the cylinder is
(A) 11 cm
(B) 5 cm
(C) 7 cm
(D) 9 cm
- Two cylinders are such that the ratio of their base radii is 2 : 1 and the ratio of their heights are 3 : 1. Then the ratio of their volumes is
(A) 6 : 1
(B) 12 : 1
(C) 5 : 1
(D) 1 : 1
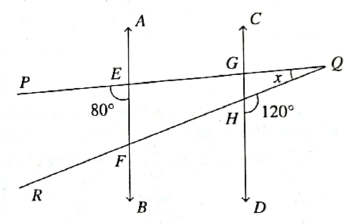
- In the given figure, AB ∣∣ CD and PQ, QR intersect AB and CD both at E, F and G, H respectively. Find the value of x.

(A) 40°
(B) 20°
(C) 30°
(D) 10°
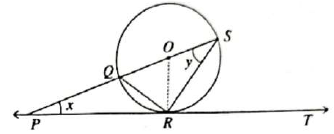
- In the given figure, PT is the tangent of a circle with centre O at point R. If diameter SQ is increased, it meets with PT at point P. If ∠SPR = x° and ∠QSR = y°, what is the value of x° + 2y°?

(A) 90°
(B) 105°
(C) 135°
(D) 180°
- An equilateral triangle CDE is constructed on a side of CD of square ABCD. The value of ∠AEB is
(A) 150°
(B) 45°
(C) 30°
(D) 20°
- A solid spherical ball of radius 4 cm is melted and recast into 64 identical spherical marbles. Then the radius of each marble is
(A) 1 cm
(B) 1.5 cm
(C) 0.2 cm
(D) 1.2 cm
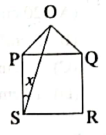
- In the given figure (not drawn to scale), PQRS is a square, ∆OPQ is an equilateral triangle, then the value of x is

(A) 20°
(B) 25°
(C) 15°
(D) 10°
- A telegraph post gets broken at a point against a storm and its top touches the ground at a distance 20 m from the base of the point making an angle 30° with the ground. What is the height of the post?
(A) 40/√3 m
(B) 20√3 m
(C) 40√3 m
(D) 30 m
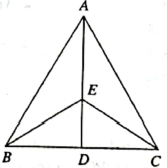
- E is point on median AD of ∆ABC. If area (∆ABE) = 10 cm² , then area(∆ACE) is

(A) 20 cm²
(B) 5 cm²
(C) 30 cm²
(D) 10 cm²
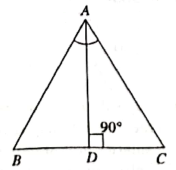
- If AD is bisector of ∠A and AD is perpendicular to BC, then ∆ABC is ____ triangle.

(A) Isosceles
(B) Equilateral
(C) Scalene
(D) None of the above
- Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter person in metres is
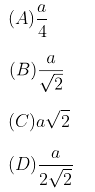
(D)
- If the radius of a circle is increased by 10%, then the percentage increased in the circumference of a circle is
(A) 10%
(B) 20%
(C) 50%
(D) 15%
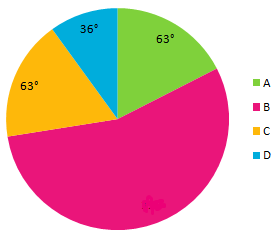
- The given pie chart (not drawn to scale) represents the annual performance of the students of a class in terms of grades A, B, C and D. The percentage of students who have got B grade is

(A) 40%
(B) 55%
(C) 60%
(D) 65%
- The ratio of the areas of a regular hexagon and a square having the same perimeter is
(A) 2√3 : 3
(B) √3 : 2
(C) 3√3 : 2
(D) 3 : 2
- The length of the longest thin rod that can fit inside a rectangular box that measures 15 cm by 10 cm by 5 cm is
(A) 18.7 cm
(B) 17.2 cm
(C) 15.8 cm
(D) 20.2 cm
- If the points (a, 0), (0, b) and (1, 1) are collinear, then which of the following is true?
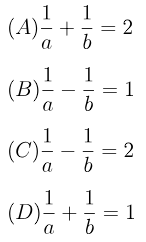
(D)
- Circle C1 passes through the centre of circle C2 and is tangential to it. If the area of C1 is 4 cm² , then the area of C2 is
(A) 8 cm²
(B) 8√π cm²
(C) 16 cm²
(D) 16√π cm²
- How many bullets can be made out of a lead cylinder 56 cm high having a radius of 6 cm, each bullet being 1.5 cm in diameter?
(A) 4000
(B) 5000
(C) 3590
(D) 3584
- The diameter of a roller is 84 cm and its length 120 cm. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in sq. m.
(A) 1632
(B) 1584
(C) 1817
(D) 1532
- A cylindrical pillar of height 7.5 m and diameter 3.5 m is to be painted. At the top and bottom, 25 cm of the pillar is covered by brass plates and the remaining portion is to be painted. Then the area of the pillar which is to be painted, is
(A) 77 m²
(B) 196 m²
(C) 86 m²
(D) 75 m²
- The perimeter of an isosceles triangle is 32 cm. Each equal side is 1½ times the base. Then the length of the equal side is
(A) 8 cm
(B) 10 cm
(C) 12 cm
(D) 14 cm
- The number of solid spheres, each of diameter 6 cm could be moulded to form a solid metal cylinder of height 45 cm and diameter 4 cm, is
(A) 3
(B) 4
(C) 5
(D) 6
- If in a triangle of base 4 cm and height 3 cm, the height is increased by 3 cm, find by how much the base should be decreased, if the new area is twice that of the original triangle.
(A) ½
(B) ¼
(C) 2
(D) 0
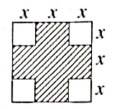
- Four equal squares are cut of a square as shown in the diagram. If the perimeter of the original square was 36 cm, then the perimeter of the shaded region is

(A) 30 cm
(B) 36 cm
(C) 32 cm
(D) 40 cm
- In a ∆ABC, it is given that ∠C = 90° and tan A = 1/√3, find the value of (sinA cosB + cosA sin B)
(A) 1
(B) ½
(C) 0
(D) 3
- If cotθ = ²⁴⁄₇ and θ is not in the first quadrant, then find the value of tanθ-secθ.
(A) 1
(B) ⁴⁄₃
(C) ³⁄₂
(D) ⁵⁄₄
- Two vertices of an equilateral triangle are origin and (4, 0). What is the area of the triangle?
(A) 4 sq. unit
(B) √3 sq. unit
(C) 4√3 sq. unit
(D) 2√3 sq. unit
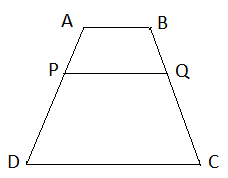
- In the following figure, ABCD is an isosceles trapezium. AB ∣∣ CD, AB = 9 cm, CD = 12 cm, AP : PD = BQ : QC = 1 : 2 . Find PQ.

(A) 11 cm
(B) 10½ cm
(C) 10 cm
(D) 4½ cm
Video Solution
WBCS Main Question Paper – 2021
1. Solve:
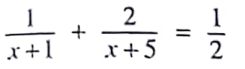
(A) 1/3
(B) ± 1/3
(C) 3
(D) ± 3
13. Find the minimum value of 5 sinθ + 12 cosθ
(A) 0
(B) -1
(C) –√3
(D) -13
20. If the length of a rectangle is increased by 30% and its width by 20%; its area will be increased by
(A) 50%
(B) 25%
(C) 56%
(D) 60%
21. The number of coconuts plucked from each tree is more than the number of coconut trees in Anil’s garden. The total number of coconuts plucked is 132. The total number of coconut trees in the garden is
(A) 12
(B) 22
(C) 11
(D) 33
24. The value of the product (a-u) (b-u) (c-u) ….. (z-u) is
(A) 25
(B) 26
(C) 0
(D) 1
29. If P = 99, then P(P² + 3P + 3) = ?
(A) 999
(B) 9999
(C) 99999
(D) 999999
31. In △ABC, D, E and F are respectively the mid-points of sides BC, CA, and AB; if △ABC=16 sq cm, then the area of the trapezium FBCE is
(A) 40 sq cm
(B) 8 sq cm
(C) 12 sq cm
(D) 24 sq cm
35. If a + 1/b = 1 and b + 1/c = 1 then find the value of c + 1/a
(A) -I
(B) 1
(C) b
(D) -b
39. The area of a regular hexagon with side 10 cm. is
(A) 50 √3 cm²
(B) 150 √3 cm²
(C) 50 cm²
(D) 300 cm²
47. The sum of opposite angles of a cyclic quadrilateral is
(A) 90°
(B) 120°
(C) 150°
(D) 180°
48. The angle between the external bisectors of two angles of a triangle is 60°, then the third angle of the triangle is
(A) 40°
(B) 50°
(C) 60°
(D) 80°
50. The length of the sides of a triangle are 5 cm, 12 cm and 13 cm. Its area is
(A) 30 cm²
(B) 37.5 cm²
(C) 60 cm²
(D) 78 cm²
56. The roots of the equation
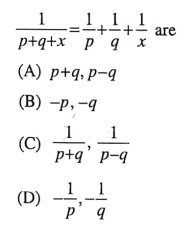
B
57. The length of the longest rod that can be put in a room of dimensions 10m x 10m x 5m is
(A) 15√3 m
(B) 15 m
(C) 10√2 m
(D) 5√3m
63. If the median drawn on the base of a triangle is half its base, the triangle will be
(A) equilateral
(B) right-angled
(C) acute-angled
(D) obtuse-angled
70. A room is 26 feet long and 10 feet wide. If its floor is to be covered by square tiles, how many minimum number of tiles will be required?
(A) 50
(B) 60
(C) 65
(D) 55
72. State in which of the following quadrants the point (√5-3, √5−2) lies.
(A) first
(B) second
(C) third
(D) fourth
75. The volume of a solid hemisphere is numerically equal to its total surface area. Its radius is
(A) 4½ units
(B) 9 units
(C) 3 units
(D) 1½ units
77. The Length of radius of spherical gas balloon increases from 7cm to 21cm as air being pumped into it. The ratio of surface areas of the balloon in two cases is
(A) 9 : 1
(B) 49 : 21
(C) 1 : 9
(D) 7 : 441
78. If area of circular field is X sq unit, perimeter is Y unit and length of diameter is Z unit, then the value of X/YZ is
(A) 1/2
(B) 1/4
(C) 1
(D) 1/8
81. What is the ratio between a square circumscribing a circle and that of the one inscribed in the circle?
(A) 2:1
(B) √2:1
(C) 2:3
(D) √2:√3
86. If cosecθ + cotθ = √3, find the value of
(A) √3/2
(B) √3
(C) 1/√3
(D) 2/√3
88.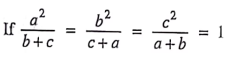
then the value of![]()
(A) 0
(B) 1
(C) -1
(D) 2
96. If cotθ = x/y, then what is the value of
![]()
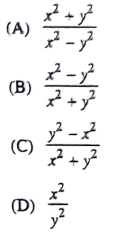
B
98. Find the angle of the elevation of the Sun when the length of shadow of a vertical pole is √3 times its height.
(A) 45°
(B) 60°
(C) 30°
(D) 22½°
101. The height of a tower is 4h meter and the height of the observer is h meter. He finds the top of the tower from a distance √3h meter from the tower. Find the angle of elevation of the tower as seen by the observer.
(A) 60°
(B) 30°
(C) 45°
(D) 75°
103. If (a, b, c) * (d, e, f) = a × f + b × c + c/d, then (5, 7, 10) * (2, 3, 2) is
(A) 6
(B) 16
(C) 26
(D) 36
105. AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and distance between them is 17 cm, then the radius of the circle is
(A) 12cm
(B) 13 cm
(C) 10 cm
(D) 11cm
109. A circular lawn has an area of 154 sq meter. A path of 7 meter width surrounds the lawn. What is the area of the lawn including the path? (in sq meter)
(A) 580
(B) 516
(C) 616
(D) 637
112. ABCD is a quadrilateral in which P, Q, R and S are the mid-points of AB, BC, CD and DA respectively. Then PQRS is
(A) trapezium
(B) parallelogram
(C) rectangle
(D) square
113.
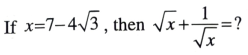
(A) 1
(B) 2
(C) 4
(D) 16
118. Two angles of a triangle are 75° and 45°. What is the value of third angle in circular measure? (as per convention, we do not use the symbol of radian.)
(A) π/2
(B) π/3
(C) π/4
(D) π/5
122.
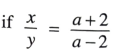 then find the value of
then find the value of
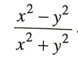
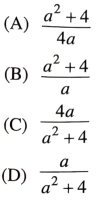
C
129. A boy recorded the weight of some of his friends as 32kg, 30kg, 40kg, 65kg, 54kg, 38kg, 36kg, 45kg, 50kg, 52kg, 40kg. What is the median?
(A) 38kg
(B) 40kg
(C) 45kg
(D) 43.8kg
133. If x/2 + y/3 = 4 and 2/x + 3/y = 1 then what is x + y equal to?
(A) 11
(B) 10
(C) 9
(D) 8
134. The distance between the centers of two circles of radii 1 cm and 7 cm is 10 cm. The length of direct tangent (in cm) is
(A) 2
(B) 6
(C) 8
(D) 18
135. In a right-angled triangle XYZ, ∠Y = 90°, if XY=2 √6 and XZ-YZ=2, then secX + tanY is
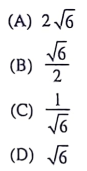
D
137. If each interior angle of a regular polygon is 144°, find the number of sides of the polygon is
(A) 10
(B) 20
(C) 24
(D) 36
140. In △ABC, ∠B= 90°, BC=7 cm, if AC-AB= 1cm, then the value of sine is
(A) 7/24
(B) 7/25
(C) 24/25
(D) 25/24
141. ![]()
then the value of K is
(A) 1/2 or 2
(B) –1 or 1/2
(C) -1/2 or 1
(D) 1/2 or -1
147. A hemisphere can with an internal radius of 9 cm is completely filled with water. Someone is requested to fill this water in a cylindrical bottle with a diameter of 3 cm and height of 4 cm. The number of bottles to be required to make the can empty is
(A) 54
(B) 128
(C) 36
(D) 256
150. If secθ=cosecΦ and 0°< (θ, Φ) < 90°, then the value of sin(θ + Φ) is
(A) 0
(B) 1/2
(C) 1/√ 2
(D) 1
156. If tanθ + secθ=4, then what is the value of cosθ ?
(A) 8/17
(B) 8/15
(C) 15/17
(D) 23/32
168. If the length of shadow on the ground of a post is 3-√3 times of its height, the angle of elevation of the Sun is
(A) 30°
(B) 45°
(C) 60°
(D) None of the above
170. If the edge of a cube is increased by 25% then percentage increase in its surface area is
(A) 25%
(B) 48-75%
(C) 50%
(D) 56.25%
177. The area of a triangle, the length of whose sides are 50m, 78m and 112m, is
(A) 1480m²
(B) 1600m²
(C) 1680m²
(D) 3360m²
181. If S=ut + 1/2ar² and u = 50, a = 9.8, t=2 the value of S is
(A) 119.6
(B) 109.8
(C) 69.6
(D) 139.2
183. If a = 999, b=998, c = 997, then the value of a³ + b³ + c³-3abc will be
(A) 8982
(B) 8980
(C) 8983
(D) 8985
186. If the surface areas of two spheres are in the ratio 4:9, then the ratio of their volumes will be
(A) 4:9
(B) 16:27
(C) 8:27
(D) 16:9
187. If sinθ: = 5/13, then what is the value of tanθ + secθ?
(A) 2.5
(B) 0.5
(C) 1.5
(D) 1.52
190. The diagonals of a rhombus are 24 cm and 10 cm. The perimeter of the rhombus (in cm.) is
(A) 68
(B) 65
(C) 54
(D) 52
192. How many more words (not necessarily meaningful) can be formed using the letters of the word RYTHM taking all at a time?
(A) 24
(B) 25
(C) 119
(D) 120
195. The area of an equilateral triangle is 400√3 sq. m. Its perimeter is
(A) 120m
(B) 150m
(C) 90m
(D) 135m
196. 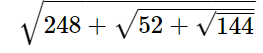 is equal to
is equal to
(A) 16.6
(B) 16
(C) 14
(D) 18.8
198. Three sets of books on Maths, Science and Social Studies have 240, 336, and 96 books in each set respectively. The books need to be stacked in such a way that all the books are stacked subject-wise and number of books in each stack is same. The total minimum number of stacks will then be.
(A) 14
(B) 48
(C) 22
(D) 21
Video Solution
WBCS Main Question Paper – 2020
- If tan 2θ tan θ = 1, then the value of tan 2θ is
(A) 1
(B) 1/√3
(C) √3
(D) None of the above
- △ABC is a triangle whose∠C = 90o. lf p is the length of the perpendicular from C to AB, then 1/BC2 + 1/AC2 =
(A) p2
(B) 2p2
(C) 1/p2
(D) 2/p2
- In the figure (not drawn to scale), a circle touches the side BC of△ABC at P and sides AB and AC produced at Q and R respectively. lf AQ = 10 cm, then the perimeter of△ABC is
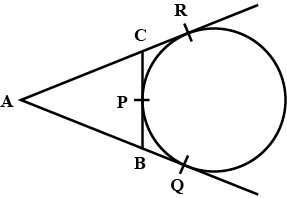
(A) 10 cm
(B) 20 cm
(C) 5 cm
(D) 25 cm
- Three solid spheres of gold whose radii are 1 cm, 6 cm and 8 cm respectively are melted into a single solid sphere. Then the radius of the sphere is
(4/3πR3)
(A) 7 cm
(B) 8 cm
(C) 9 cm
(D) 10 cm
- A conical container of base diameter 2R and height H is full of water which is poured into a cylindrical container of diameter 2pR, then it will occupy a height equal to
(1/3π x r2h)
(A) 3p2H
(B) H/3p
(C) pH/3
(D) H/3p2
- In the given figure, (not drawn to scale)△ABC is a right angled triangle,∠B=90o, AB = 6 cm and BC = 8 cm, the value of r is
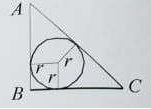
(A) 1 cm
(B) 2 cm
(C) 2.5 cm
(D) 3 cm
- A right circular cone, a right circular cylinder and a hemisphere, all have the same radius and the heights of cone and cylinder equal their diameters. Then their volumes are proportional respectively to
(A) 2 : 1 : 3
(B) 1 : 3 : 1
(C) 1 : 2 : 3
(D) 3 : 2 : 1
- In a triangle PQR, points A, B and C are the mid points of the sides PQ, QR and RP respectively. If the area of the triangle ABC is 16 sq.units, then the area of the triangle PQR is
(64 sq unit)
(A) 32 sq.unit
(B) 48 sq.unit
(C) 50 sq.unit
(D) None of the above
- The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, then the distance of the other chord from the centre is
(A) 5 cm
(B) 4 cm
(C) 3 cm
(D) 2 cm
- If a = 2021, b = 2022, c = 2023, then the value of a3+ b3+ c3 – 3abc is
(A) 18198
(B) 20158
(C) 19288
(D) 19188
- If α and ß be the roots of the quadratic equation ax2+ 2bx + c = 0 and α + y, ß + y be those of Ax2+ 2Bx + C = 0, then which one is correct ?
(A) A2(B2 – AC) = a2(b2 – ac)
(B) A2(b2 – ac) = a2(B2 – AC)
(C) b2(A2 – BC) = B2(a2 – bc)
(D) B2(A2 – BC) = b2(a2 – bc)
- If 2x2+ 5y2+ 2z2 – 2xy – 6yz = 0, then x : y : z is
(A) 1 : 2 : 3
(B) 2 : 1 : 3
(C) 2 : 3 : 4
(D) 3 : 2 : 4
- If a2+ b2+ c2 = ab + bc + ca, then which one is correct ?
(A) a + b + c = 0
(B) a = b = c
(C) a – b – c = 0
(D) None of the above
- If a + b + c = 0, then
![]()
is equal to
(A) abc
(B) 1/abc
(C) 0
(D) 1
- If the semi perimeter of a right-angled triangle be s cm and hypotenuse be c cm, then the area of the triangle is
(A) s/s-c sq.cm
(B) sc sq.cm
(C) s(s-c) sq.cm
(D) None of the above
- If tanθ + sinθ = m and tanθ – sinθ = n, then which one is correct ?
(A) m2 + n2 = 2√mn
(B) m2 – n2 = 4mn
(C) m2 – n2 = 4√mn
(D) m2 – n2 = 2√mn
- The radius of a solid sphere is R cm. It is bisected, then the total surface area of the two pieces obtained is,
(A) 5πR2 sq.cm
(B) 4πR2 sq.cm
(C) 6πR2 sq.cm
(D) 3πR2 sq.cm
- Ifx – 5 + 2√6, then
![]()
is equal to
(A) 5
(B) 864
(C) 973
(D) 874
- Ifx = by + cz,y = cz + ax and z = ax + by, then
![]()
is equal to
(A) 0
(B) 1
(C) 1/abc
(D) abc
- A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8 : 5, the ratio of radius to the height is
(A) 3 : 5
(B) 3 : 4
(C) 4 : 5
(D) 2 : 1
- ABCD is a cyclic quadrilateral and the sides DC and AB, are produced to meet at P. If ∠APD=25o and∠BPC=70o then ∠BAD is equal to
(A) 25°
(B) 70°
(C) 95°
(D) 85°
67.
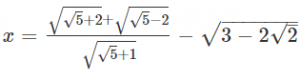
then x equals to
69.
![]()
then the value of x¯ (mean) is
(A) 10
(B) 25
(C) 20
(D) 27
- Lateral surface area of a right circular cone is three times the volume of that cone. If the height and the radius of the cone are h unit and r unit respectively, then
![]()
is equal to
(A) 1
(B) 3
(C) 9
(D) 1/9
- A hemispherical bowl is made of steel sheet 0.8 cm thick. The inside radius of the bowl is 5 cm. Volume of steel used in making it is
(A) 146 cm³
(B) 144.9 cm³
(C) 146.9 cm³
(D) 148.6 cm³
72.
![]()
then which one is correct ?
(A) x + y = a
(B) x3 + y3 = b3
(C) x2 + y2 = a2
(D) None of the above
- The greatest and the least value ofa + b sinθ (0°≤ θ ≤90°) a+bsinθ(0°≤ θ ≤90°) are 7 and 3 respectively. The value of a and b are
(A) a = 2, b = 5
(B) a = 3, b = 4
(C) a = 0, b = 7
(D) a = 3, b = 7
- If P(1, 2), Q(4, 6), R(5, 7) and S(a, b) are the vertices of a parallelogram PORS, then the values of a and b are
(A) a = 2, b = 6
(B) a = 1, b = 5
(C) a = 2, b = 3
(D) a = 6, b = 7
- If H, S, V be the height, curved surface area and volume of a cone respectively, then the value of
![]()
(A) 0
(B) 1
(C) ππ
(D) π³π³
79.
![]()
is equal to
(A) 1
(B) 2
(C) 8ab
(D) 4ab
80.
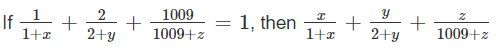
is equal to
(A) 0
(B) 1
(C) 2
(D) 3
- The areas of two similar triangles are 36 sq.cm and 81 sq.cm respectively. If the median of smaller triangle is 12 cm then the corresponding median of the larger triangle is
(A) 12 cm
(B) 18 cm
(C) 24 cm
(D) 10 cm
93.
![]()
then the value of
![]()
(A) 0
(B) 1
(C) 2020
(D) 2016
- If 3sinα + 5cosα = 5, then the value of (3cosα – 5sinα)² is equal to
(A) 9
(B) 25
(C) 9595
(D) None of the above
- Two circles with radiir1 andr2 respectively, touch each other externally. Let R be the radius of a circle that touches these two circles as well as a common tangent to the two circles, which of the following is true ?
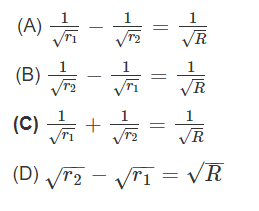
C
- The mean of a frequency distribution is 8.1,
![]()
then the value of k is
(A) 2
(B) 4
(C) 5
(D) 6
- Three cubes of edges 6 cm, 8 cm and 10 cm are melted without loss of metal into a single cube. The edge of the new cube will be :
(A) 16 cm
(B) 14 cm
(C) 12 cm
(D) 8 cm
- From a group of 7 men and 6 women, five persons are to be selected to form a committee so that at least 3 men are there in the committee. In how many ways can it be done ?
(A) 624
(B) 209
(C) 756
(D) 212
- If(a, b) ∗ (c, d) = (a + d) − c/b then
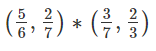
will be
(A) 1
(B) 0
(C) 7
(D) 2
- Simplify :
![]()
(A) 3/5
(B) 2/5
(C) 3/4
(D) 1/3
136.
![]()
then the value of n will be
(A) 5
(B) 4
(C) 2
(D) 3
- A box contains 15 marbles out of which 4 are white, 5 are red and 6 are blue. Three balls are to be drawn at random from the bag. What is the probability that all of them are red ?
(A) 1/22
(B) 2/89
(C) 2/77
(D) 2/91
- A problem is given to three students whose chances of solving it are 1/2, 1/3 and 1/4 respectively. What is the probability that the problem will be solved ?
(A) 1/4
(B) 1/2
(C) 3/4
(D) 7/12
- How long will a boy take to run round a square field of side 35 meters, if he runs at the rate of 9 km/hr ?
(A) 40 sec
(B) 50 sec
(C) 56 sec
(D) 54 sec
- The ratio of the no. of white balls in a bag to that of black balls is 1 : 2. If 9 grey balls are added the ratio of nos. of white, black and grey becomes 2 : 4 : 3. How many black balls were in the bag ?
(A) 6
(B) 9
(C) 12
(D) 8
200.
![]()
will be
(A) 1/x
(B) -1/x
(C) x
(D) −x
Video Solution
WBCS Main Question Paper – 2018
2. If a square and a rectangle having the same perimeter and their areas are S and R respectively then
(A) S = R
(B) S > R
(C) S < R
(D) None of the above
3. A parallelogram, a rectangle and triangular region stands on same base and between same parallel and if their area are P, R and T respectively, then
(A) P = R = 2T
(B) P = R = T/2
(C) 2P = 2R = T
(D) P = R = T
5. If x3 + 6x2 + 4x + K is divisible by (x + 2), then the value of K is
(A) – 6
(B) – 7
(C) – 8
(D) – 10
6. Which of the following geometric figure has diagonals equal in length ?
(A) Parallelogram
(B) Rhombus
(C) Trapezium
(D) Rectangle
12. Two equations 3x + 6y = 15 and 6x + 12y = 30 have
(A) only one solution
(B) infinite number of solution
(C) no solution
(D) None of the above
14. The measures of two angles of a triangle are 35°57’4″ and 39°2’56”, then circular value of third angle is
(A) 7π / 12
(B) π / 20
(C) 5π / 12
(D) π
15. If the length of shadow on the ground of a post is √3 times of its height, the angle of elevation of the Sun is
(A) 30°
(B) 45°
(C) 60°
(D) None of the above
16. If the numerical values of total surface area and volume of a cube are equal, then the length of its diagonal is
(A) 6√3
(B) 6
(C) 6√2
(D) 3√6
22. A hemisphere can with internal radius of 9 cm is completely filled with water. Someone is requested to fill this water in a cylindrical bottle with a diameter of 3 cm and height of 4 cm. The number of bottles to be required to make the can empty is
(A) 54
(B) 128
(C) 36
(D) 256
23. The Length of radius of spherical gas balloon increases from 7 cm to 21 cm as air being pumped into it. The ratio of surface areas of the balloon in two cases is
(A) 9 : 1
(B) 49 : 21
(C) 1 : 9
(D) 7 : 441
37. What is the volume of the cube (in cubic cm) whose diagonal measures 4√3 cm ?
(A) 8
(B) 16
(C) 27
(D) 64
52. If the length of radius of a right circular cylinder is doubled and height is halved, the lateral surface area will be
(A) equal
(B) double
(C) half
(D) 4 times
53. The length of a radius of a circle is 13 cm. and the length of a chord of the circle is 10 cm., the distance of the chord from the center of the circle is
(A) 12.5 cm.
(B) 12 cm.
(C) √69 cm.
(D) 24 cm.
54.
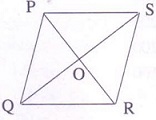
The diagonals PR and QS of the rhombus intersect each other at the point O. What is the value of ∠POS∠POS ?
(A) Insufficient information
(B) 90°
(C) Any angle
(D) 45°
55. If (0,0), (4, -3) and (x, y) are collinear then
(A) x = 8, y = – 6
(B) x = 8, y = 6
(C) x = 4, y = – 6
(D) x = – 8, y = 6
56.
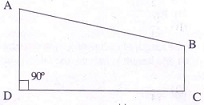
In the above figure AD | | BC, AD = 10 cm, BC = 5cm, CD = 10 cm. The area of ABCD is
(A) 150 sq.cm
(B) 75 sq.cm
(C) 500 sq.cm
(D) 250 sq.cm
60. If area of circular field is X sq. unit, perimeter is Y unit and length of diameter is Z unit then the value of X/YZ is
(A) 1/2
(B) 1/4
(C) 1
(D) 1/8
63. A circular lawn has an area of 154 sq. meter. A path of 7 meter width surrounds the lawn. What is the area of the lawn including the path ? (in sq. meter)
(A) 580
(B) 516
(C) 616
(D) 637
70. The area of a circle is 2464 square meters. What will be its circumference ?
(A) 132 m
(B) 176 m
(C) 231 m
(D) 272 m
87. The poles of heights 6m and 11m stand vertically on a plane ground. If the distance between their feet is 12m, what is the distance between their tops ?
(A) 12.8m
(B) 13m
(C) 14m
(D) 15m
91. A circular copper wire of radius 7 cm is bent to form a rectangle. If breadth and length of the rectangle are in the ratio of 4 : 7 respectively, what is the breadth of the rectangle ? (in cm.)
(A) 8 cm.
(B) 14 cm.
(C) 10 cm.
(D) 12 cm.
96. A horse is tied to a post by a rope. If the horse moves along a circular path, always keeping the rope tight and describes 88 m when it traces 72° at the centre, then the length of the rope is
(A) 35m
(B) 70m
(C) 17.5m
(D) 22m
45. A river 1.5 m deep and 36 m wide is flowing at the rate of 3.5 km per hour. The amount of water that runs into the sea per minute (in cubic meter) is
(A) 3150
(B) 31500
(C) 6300
(D) 63000
97. What value of m for which two roots of the quadratic equation 4×2 + 4(3m – 1)x + (m + 7) = 0 are reciprocal to each other ?
(A) – 7
(B) 7/4
(C) – 3
(D) 1/3
100. If x = 2 + √3 the value of x + 1/x is
(A) 2
(B) 2√3
(C) 4
(D) 2–√3
Video Solution